Black Parade

Mengoperasikan Kapasitor Motor Induksi 3-Fasa pada Sistem Tenaga 1-Fasa

Ragil Rahmadi
Teknik Industri, Universitas Gunadarma, Jakarta
Email: RagiRahmadi@rocketmail.com


ABSTRAK
Langkah-langkah pengoperasian motor induksi 3-fasa pada sistem tenaga listrik 1-fasa dengan menggunakan kapasitor telah berkembang dengan baik. Metode ini digunakan karena mempunyai respon kecepatan yang cepat pada motor, arus start yang kecil dan perbaikan faktor daya hingga mendekati satu. Karakteristik motor saat beroperasi tergantung dari letak dan nilai kapasitor jalan yang digunakan pada motor. Penelitian ini dimaksudkan untuk membuatkan metode baru dalam meletakkan dan memilih kapasitor jalan untuk mengoperasikan motor induksi 3-fasa pada sistem tenaga listrik 1-fasa. Data motor yang digunakan adalah motor induksi 3-fasa 1,5 kW; 220/380V; ∆/Y; 50 Hz; 6,2/3,6A; 1400 rpm; kelas B; faktor daya 0.84 tertinggal. Hasil penelitian menunjukkan bahwa motor bekerja lebih baik dan lebih efisien jika kapasitor jalan diletakkan pada sisi kumparan dengan impedansi yang lebih besar. Motor dapat bekerja dengan menggunakan kapasitor 25,9 µ F pada beban 95,14%, kecepatan 1400 rpm, faktor daya 0,99 mendahului, dengan distorsi harmonik arus yang lebih rendah.

Kata kunci: rangkaian kapasitor, nilai kapasitansi, daya semu pada motor (VA) Teknik Industri Gunadarma 2009 Teknik Tenaga Listrik.


PENDAHULUAN

Pengoperasian motor induksi 3-fasa pada sistem tenaga listrik AC 1-fasa sangat dibutuhkan pada
daerah pertanian, industri kecil dan daerah tertentu yang hanya mempunyai sistem tenaga listrik 1-fasa, sedangkan mereka membutuhkan motor penggerak dengan daya yang besar (motor induksi 3-fasa) yang secara normal harus dioperasikan pada sistem tenaga listrik 3-fasa [1,2]. Salah satu cara agar motor induksi 3-fasa dapat digunakan dengan baik pada kondisi ini adalah dengan mengoperasikan motor induksi 3-fasa pada sistem tenaga listrik 1-fasa dengan menggunakan kapasitor [1,3].

Dalam sistem pengoperasian motor induksi 1-fasa, kapasitor boleh diletakkan pada sisi kumparan bantu (impedansi lebih besar) atau pada sisi kumparan utama (impedansi lebih) asal kapasitor yang digunakan dapat menggerakkan motor [4]. Berdasarkan kondisi ini, maka penelitian ini dimaksudkan untuk merancang metode baru dalam mengoperasikan
motor induksi 3-fasa pada sistem tenaga 1-fasa dengan cara menempatkan kapasitor pada sisi kumparan dengan impedansi yang lebih besar (kumparan bantu).

Secara umum, untuk mengoperasian motor induksi 3-fase pada sistem tenaga 1-fase dengan menggunakan kapasitor dapat dilakukan dengan


cara mengubah bentuk rangkaian kumparan motor induksi 3-fase menjadi seperti rangkaian motor induksi 1-fase jenis motor kapasitor, seperti yang ditunjukkan pada Gambar 1.

Gambar 1. Bentuk pengoperasian motor induksi pada sistem 1-phasa: (a) motor kapasitor (b) metode yang digunakan Scheda [2] (c) metode yang digunakan Smith [4]

Pengaruh besarnya arus yang melewati kapasitor (IC) terhadap tegangan yang diberikan pada kapasitor (VC) dapat dibuatkan sebagai berikut.
C C I = ω.C..V.....................................................................(1)
dengan :
ω = 2.(3,14).( f )
f = frekuensi sumber (Herz)
C = kapasitansi kapasitor (Farad)

Bila diinginkan motor induksi 3-fasa bekerja pada sistem tenaga 1-fasa tanpa melewati batas arus nominal kumparannya (Iph), maka nilai kapasitansi kapasitor (C) yang dipakai adalah:
.............................................................................(2)
Besarnya daya reaktif (VARC) yang disumbangkan kapasitor C adalah :
VARC = VC x IC..................................................................(3)
VARC ini akan menjadi daya semu (VA) motor
induksi 3-fasa saat beroperasi pada sistem tenaga 1 fasa.

Bila VAR3ph merupakan daya reaktif motor saat beroperasi pada sistem tenaga 3-fasa, maka besarnya daya reaktif motor induksi saat beroperasi pada sistem tenaga 1-fasa (VARM) adalah:
VARM = VARC3h – VARC..................................................(4)
Kemudian besarnya arus (IL), faktor daya (cos) dan daya masukan motor (PL) saat beroperasi pada sistem tenaga 1-fasa adalah:
.........................................................................(5)
......................................................................(6)
...................................................................(7)
...............................................................(8)

Bila digunakan kapasitor start pada sisi kumparan bantu untuk menstart motor induksi 3-fasa pada sistem tenaga 1-fasa, maka besarnya nilai reaktansi kapasitif dari “kapasitor-start” untuk menstart motor dapat dicari berdasarkan besarnya nilai torsi start maksimum dengan mengacu ke persamaan di bawah ini [7].
............................................................(9)
Atau dapat juga dengan pemilihan torsi start maksimum per amper[7] seperti rumus dibawah
ini[8]
..............................................(10)
dengan :
Xc = reaktansi kapasitif dari kapasitor start yang akan digunakan
Xa = reaktansi induktif dari kumparan bantu
Xm = reaktansi induktif dari kumparan utama
Ra = tahanan dari kumparan bantu
Rm = tahanan dari kumparan utama
Zm = impedansi kumparan utama

Untuk memperoleh nilai Xc yang sesungguhnya dari kapasitor yang digunakan, harus diperoleh dahulu nilai impedansi dasar dari motor induksi yang digunakan dengan menggunakan rumus sebagai berikut.
.......................................................................... (11)

dengan :
V = tegangan sumber 1-fase yang digunakan
VA = daya semu motor induksi 3-fase yang digunakan
Selanjutnya akan diperoleh nilai reaktansi kapasitif sebenarnya sebesar.
Xc =(Xc(pu)). (Zd)...........................................................(12)

Besarnya nilai kapasitor start (Cs) yang dibutuhkan selanjutnya dapat diperoleh dengan menggunakan persamaan berikut.
(satuan, Farad)...........................................(13)
dengan :
f = frekuensi sumber
π = 3,141593


METODE PENELITIAN

Penelitian ini merupakan perancangan metode baru dalam mengoperasikan motor induksi 3- fasa pada sistem tenaga 1-fasa dengan meletakkan kapasitor jalan pada sisi kumparan dengan impedansi yang lebih besar (kumparan bantu). Untuk melihat kinerja motor induksi 3 fasa saat beroperasi pada sistem tenaga 1-fasa, maka motor diujicoba di laboratorium dengan menggunakan metode yang diusulkan, kemudian dibandingkan dengan kinerja motor saat beroperasi normal pada sistem tenaga 3-fasa dan saat beroperasi dengan menggunakan metode yang lama (meletakkan kapasitor yang sama pada sisi kumparan dengan impedansi yang lebih kecil). Bentuk rangkaian kapasitor yang dipasang pada kumparan motor induksi 3fasa dengan menggunakan metode usulan diperlihatkan pada Gambar 2, dimana Cs adalah
kapasitor start dan Cr adalah kapasitor jalan.


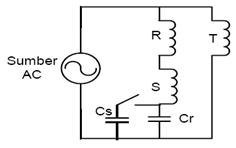
Gambar 2. Bentuk rangkaian kapasitor yang dipasang pada kumparan motor induksi 3-fasa

Data motor induksi yang digunakan pada penelitian ini adalah motor induksi 3-fase 1,5kW, 220/380V; 50Hz; 6,2/3,6A; 1400 rpm dengan faktor daya 0,84 tertinggal. Peralatan pendukung yang digunakan pada penelitian ini adalah:
1. Generator sinkron 1-fasa, 3kW (sebagai beban motor yang dikopel langsung dengan motor)
2. Lampu pijar berbagai ukuran, sebagai beban generator.
3. Kapasitor jalan (25.9 uF) dan kapasitor start (49,8 uF)
4. Meja panel, sebagai sumber tenaga
5. Fluke 434 power quality analyzer, sebagai alat ukur
6. Multimeter digital, sebagai alat ukur
7. Rpm meter, sebagai alat ukur kecepatan rotor motor induksi
8. Saklar dan perlengkapannya

Bentuk bagan alir penelitian diperlihatkan pada
Gambar 3 dan bentuk penempatan alat ukur dalam mengoperasikan motor induksi 3-fasa pada sistem tenaga listrik 3-fasa dan pada sistem tenaga listrik 1-fasa diperlihatkan pada Gambar 4.



Gambar 3. Bagan alir penelitian

a) Pengoperasian pada sistem tenaga 3-fasa


b) Pengoperasian pada sistem tenaga 1-fasa


Gambar 4. Penempatan alat ukur dalam mengoperasikan motor induksi 3-fasa pada: a) sistem tenaga listrik 3-fasa dan b) sistem tenaga listrik 1- fasa


HASIL DAN PEMBAHASAN

Data Hasil Penelitian
Data hasil penelitian bentuk hubungan kinerja motor saat diberikan perubahan beban pada motor diperlihatkan pada Gambar 5 sampai dengan Gambar 8 dan tabel 1, dengan keterangan gambar sebagai berikut.
mtd1 = kondisi motor saat beroperasi pada sistem 1-fasa dengan menggunakan metode usulan dengan meletakkan kapasitor pada sisi kumparan dengan impedansi yang lebih besar
1LM = kondisi motor saat beroperasi pada sistem 1-fasa dengan menggunakan metode lama dengan meletakkan kapasitor pada sisi kumparan dengan impedansi yang lebih kecil
3fs = kondisi motor saat beroperasi pada sistem 3-fasa

Gambar 5. Hubungan arus saluran terhadap daya keluaran pada motor



Gambar 6. Hubungan faktor daya terhadap daya keluaran pada motor



Gambar 7. Hubungan efisiensi terhadap daya keluaran pada motor



Gambar 8. Hubungan kecepatan terhadap daya keluaran pada motor




Menentukan Nilai kapasitor

Kapasitor yang digunakan pada penelitian ini diserikan dengan dua kumparan motor (kumparan R dan S, perhatikan Gambar 2. Pada kondisi ini nilai reaktansi kapasitif yang dibutuhkan kapasitor jalan adalah setengah dari nilai persamaan 2. Bila diberikan tegangan sumber ’Vs’ pada kapasitor, maka diperoleh nilai kapasitansi kapasitor yang digunakan sebesar:
(14)

Bila mengacu kepada data motor yang digunakan, maka diperoleh hasil perhitungan nilai kapasitor jalan dari persamaan 14 sebesar C= 26,045 μF, tetapi karena susah mendapatkan nilai kapasitor yang sesuai di pasaran, maka pada penelitian ini digunakan nilai C = 25,9 μF. Untuk tenaga penggerak awal yang besar, maka diperlukan kapasitor start pada motor. Dengan menggunakan program persamaan 9 dan 10 dapat dicari nilai reaktansi kapasitor start yang baik untuk mengerakkan motor. Bila digunakan program Matlab dan dengan mevariasikan nilai reaktansi kapasitor start (dalam sistem per-unit, pu), maka diperoleh gambaran variasi nilai torsi yang dihasilkan kapasitor start seperti yang diperlihatkan pada Gambar 9.

Dari hasil simulasi Gambar 9 terlihat bahwa torsi start maksimum diperoleh saat nilai Xc=2 pu dan torsi start maksimum per-amper diperoleh saat nilai Xc=2,5 pu. Selanjutnya, dengan memasukkan data motor induksi 3-fasa ke persamaan 11, maka untuk tegangan 220V diperoleh nilai Xd=20,247 ohm. Dengan memasukan nilai Xd ini ke persamaan 12, maka diperoleh nilai Xc=40,85 ohm (untuk torsi start maksimum) dan Xc=51,07 ohm (untuk torsi start maksimum per-amper). Selanjutnya, dengan memasukkan nilai Xc ini ke persamaan 13, maka diperoleh nilai kapasitansi kapasitor start sebesar 77,92μF untuk torsi start maksimum dan 62,33μF untuk torsi start maksimum per-amper. Agar motor dapat distart optimal maka nilai kapasitansi kapasitor start sebaiknya berada dalam batasan antara kedua nilai ini. Dalam penelitian ini dipilih nilai total kapasitansi kapasitor start sebesar 75,7μF.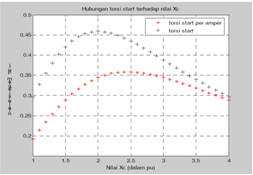


Gambar 9. Prilaku torsi start untuk berbagai nilai reaktansi kapasitif kapasitor

Validasi Hasil Perhitungan

Dengan memperhatikan persamaan 2 dan 14 terlihat bahwa tegangan pada kapasitor adalah sebesar 2 kali tegangan sumber (Vc=2Vs). Tegangan sumber yang terukur pada penelitian ini adalah 222V, dan dengan memasukkan data ini dan data kapasitor yang digunakan pada persamaan 3 akan diperoleh nilai VARC=1604,04 VAR, yang sekaligus menjadi daya semu motor saat dioperasikan pada sistem tenaga listrik 1-fasa. Selanjutnya dari persamaan 4 sampai dengan (8) akan diperoleh nilai VARM= 158,55 VAR, IL=7,23A, faktor daya (cos ф)=0,995 mendahului dan daya masukan motor (PL) = 1596,02W. Jika dibandingkan hasil perhitungan ini dengan kenyataan hasil yang terukur oleh alat ukur dimana IL=7A, faktor daya=0,99 mendahului dan PL=1538,46W, maka terjadi faktor kesalahan dalam perhitungan (fk) sebesar: IL(fk)=3,18% (untuk arus masukan), Pf(fk)=0,5% (untuk faktor daya) dan PL(fk)=3,6% (untuk daya masukan). Dari hasil ini terlihat bahwa tingkat kesalahan rumus yang diberikan untuk metode yang diusulkan masih di bawah 5% sehingga masih layak untuk digunakan.

Analisa Hasil

Dari hasil tabel 1 dan grafik 5 sampai dengan grafik 8 yang telah diberikan terlihat bahwa motor induksi 3-fasa saat beropeasi pada sistem tenaga 1-fasa dengan menggunakan metode usulan mampu bekerja dengan kecepatan standard (1400 rpm) pada beban 95,14% dari beban penuh 3-fasanya. Walaupun demikian, tidak disarankan pada kondisi ini karena arus yang melewati kumparan motor telah jauh melebihi arus nominalnya (arus yang melewati kumparan sebesar 5.4A, sedangkan arus nominal motor sebesar 3,6A). Kinerja yang terbaik bagi motor adalah mengoperasikannya pada beban 82,85% dari beban penuh 3-fasanya yang bekerja pada kecepatan 1425 rpm. Pada kondisi ini faktor daya motor naik hingga mendekati 1 (0,99 mendahului) dengan efisiensi sedikit lebih baik dari efisiensi 3-fasanya. Sementara itu, Total Current Harmonik Distortion (THDi) yang terjadi pada motor juga turun saat dioperasikan pada sistem tenaga listrik 1-fasa (dari 12,1 menjadi 11,5). Ini terjadi karena disamping kapasitor memperbaiki faktor daya motor, kapasitor yang dipasang pada kumparan motor juga membentuk filter harmonik yang dapat memperkecil pengaruh harmonik yang timbul.

Jika dibandingkan hasil dari metode yang dibuat (yang diusulkan) dengan metode lama (dengan menggunakan nilai kapasitor jalan yang sama, tetapi dengan meletakkan kapasitor pada sisi kumparan dengan impedansi yang kecil), maka terlihat bahwa metode yang dibuat lebih baik dari metode yang lama. Menaikan kemampuan metode lama dapat dilakukan dengan menaikkan nilai kapasitansi kapasitor jalannya. Tetapi, keputusan ini akan membahayakan pada motor karena dengan memperbesar nilai kapasitansi kapasitor akan memperbesar amplitude arus yang melewati kumparan motor (lihat persamaan 1 sehingga dapat memperpendek umur motor. Jadi dengan menggunakan metode usulan, maka nilai kapasitansi kapasitor jalan yang digunakan akan lebih kecil, sehingga akan lebih menghemat biaya.

KESIMPULAN

Berdasarkan hasil penelitian dan pembahasan, maka diperoleh kesimpulan sebagai berikut.
1. Metode yang diusulkan untuk merancang kapasitor jalan dalam mengoperasikan motor induksi 3-fasa pada sistem tenaga 1-fasa dapat bekerja pada beban 91,14% beban penuh 3-fasanya pada kecepatan standarnya (1400rpm). Walaupun demikian, kondisi yang terbaik adalah mengoperasikan motor dengan beban 82,85% dari beban penuh 3-fasanya.
2. Motor dapat beropersi dengan metode usulan dengan faktor daya yang mendekati satu (0,99), THDi yang lebih kecil, dan dengan efisiensi yang lebih tinggi dari keadaan normal.
3. Rumus yang diberikan untuk menghitung nilai kapasitor yang tepat pada metode usulan mempunyai tingkat keakuratan yang tinggi terhadap hasil percobaan, sehingga sangat layak digunakan.
4. Metode yang diberikan mempunyai kinerja lebih baik dan lebih efisien dari metode lama yang umum digunakan karena hanya menggunakan nilai kapasitansi kapasitor yang lebih kecil dengan kemampuan yang lebih besar.


REFERENSI

[1] Anthony Zuriman dan Efendi Asnal, “Sistem pengaman motor induksi 3-fasa terhadap gangguan hubung singkat satu fasa dengan cara merubah sumber tegangan”, Prosiding SNVMS 2004, ISBN: 979-96964-1-0, 2004, hal. 643-649.
[2] Scheda, “Perencanaan kapasitor start untuk mengoperasikan motor induksi 3-fase pada sistem tenaga 1-fase”, Jurnal Momentum, Vol. 2 No. 2, Agustus 2004, hal. 9-13.
[3] Anthony Zuriman, “Perancangan sistem kendali dual fungsi pengoperasian motor induksi 3-fasa”, Jurnal Momentum, Vol. 3 No. 2, Agustus 2005, hal. 58-63.
[4] Smith, Tumiran dan Berahim Hamzah, “Kinerja pengoperasian motor induksi 3-fasa pada sistem tenaga 1-fasa dengan menggunakan kapasitor”, Jurnal Teknosain, Terakreditasi No. ISSN: 1411-6162, Jilid 16. No. 1, Januari 2003, UGM, Yogyakarta, 2003, hal. 1-12.

Arus Listrik

Arus listrik (I) yang mengalir melalui penghantar didefinisikan sebagai banyaknya muatan listrik (Q) yang mengalir setiap satu satuan waktu (t).

Secara matematis dapat dituliskan:
I = arus listrik (A)
Q = muatan listrik (C)
t = selang waktu

Contoh cara menghitung arus listrik:

Pada suatu penghantar mengalir muatan listrik sebanyak 60 coulomb selama 0,5 menit.

Hitung besar arus listrik yang mengalir pada penghantar tersebut ?

Penyelesaian:
Diketahui: Q = 60 C
t = 0,5 menit
= 30 sekon
Ditanyakan: I = ........ ?
Dijawab:

I = 60 / 30

I = 2 ampere

Jadi besar kuat arus listrik yang mengalir pada penghantar 2 ampere

Hukum Ohm

Hukum ohm digunakan untuk menentukan hubungan arus listrik dan tegangan dalam sebuah hambatan.
Hukum ohm sendiri berbunyi: “Kuat arus yang melalui penghantar sebanding dengan beda potensial pada kedua ujung penghantar”.

Misalnya pada sebuah rangkaian yang terdiri lampu dan baterai, lampu yang dinyalakan dengan satu buah baterai akan menyala redup, dengan tiga baterai lebih terang, karena arus yang mengalir lebih besar. Jadi semakin besar beda potensial semakin besar pula arus listrik yang dihasilkan

Nilai perbandingan beda potensial dengan arus listrik yang mengalir merupakan nilai resistansi (hambatan) yang dimiliki oleh penghantar dan nilainya tetap. Secara matematis hukum ohm dapat ditulis :

V / I = R

atau

V = I . R

R = hambatan listrik, satuan ohm (W)

Satuan hambatan listrik yang lebih besar dinyatakan dalam kilo ohm (kW) atau mega ohm (MW).
1 kilo ohm = 103 ohm

1 mega ohm = 106 ohm

Contoh cara menghitung kuat arus listrik dengan hukum ohm:

Sebuah aki yang mempunyai tegangan 12 volt dipakai untuk menyalakan lampu yang mempunyai hambatan 60 W, berapa kuat arus yang mengalir pada lampu ?

Penyelesaian:
Diketahui: V = 12 volt
R = 60 W
Ditanyakan: I = ........ ?
Dijawab:

I = V / R = 12 / 60

Jadi besar kuat arus listrik yang mengalir pada lampu 0,2 ampere.

Hukum I Kirchoff

Hukum I Kirchoff digunakan untuk Menghitung Kuat Arus pada Rangkaian tidak Bercabang

Hukum kirchoff berbunyi:

“Pada rangkaian listrik tak bercabang, kuat arus di setiap titik pada rangkaian sama besar”.

Pada rangkaian listrik seperti gambar di samping, arus listrik keluar dari kutub positif sumber tegangan lalu mengalir melalui ampermeter A → ampermeter B → lampu → ampermeter C → ampermeter D → kutub negatif sumber tegangan. Didalam rangkaian tidak terdapat percabangan, sehingga kuat arus yang ditunjukkan oleh ke empat ampermeter sama besar atau I₁ = I₂ = I₃ = I₄

Hukum kirchoff untuk arus listrik bercabang berbunyi:

“jumlah kuat arus yang masuk pada titik percabangan sama dengan jumlah kuat arus yang keluar dari titik percabangan tersebut”.

Pernyataan ini dikenal sebagai Hukum I Kirchoff, Secara matetatis dapat ditulis :

I_masuk = I_keluar

Secara skematik rangkaian bercabang terlihat sperti di bawah ini:

Pada rangkaian di samping, arus listrik keluar dari kutub positif sumber tegangan mengalir melalui ampermeter A (I₁)→ pada titik cabang X arus terbagi menjadi I₂ dan I₃. Pada titik cabang Y arus bergabung lagi menjadi I4 → ampermeter D → kutub negatif sumber tegangan.

Kkuat arus yang ditunjukkan ampermeter A sama dengan yang ditunjukkan ampermeter B ditambah ampermeter C, atau dapat ditulis I₁ = I₂ + I₃ sedangkan penunjukkan ampermeter D sama dengan ampermeter A.

Contoh menghitung arus listrik bercabang:

Jika besar kuat arus I = 10 ampere, I₁ = I₃ = 3 ampere. Hitung besar kuat arus I₂ ?

Penyelesaian:
Diketahui: I = 10 A
I₁ = I₃ = 3 A
Ditanyakan: I₂ = ........ ?

Dijawab:

I₁ = I₂ + I₃ + I₄
10 = 3 + I₂ + 3
10 = 6 + I₂
I₂ = 4
Jadi besar kuat arus listrik yang mengalir pada I2 adalah 4 ampere.

Rangkaian Resistor

Rangkaian resistor digunakan untuk mendapatkan suatu nilai dari beberapa resistor. Rangkaian resistor terdiri dari rangkaian seridan rangkaian paralel.

1. Rangkaian Resistor Seri

Resistor yang disusun seri selalu menghasilkan resistansi yang lebih besar.
Pada rangkaian seri, arus yang mengalir pada setiap resistor sama besar.
R₁, R₂, dan R₃ disusun secara seri, resistansi dari gabungan R₁, R₂, dan R₃ dapat diganti dengan satu resistor pengganti yaitu R_s.

Resistor yang dirangkai secara seri mempunyai nilai pengganti, yang besarnya dapat dirumuskan: Jika semua nilai R yang disusun sama, dapat ditulis:

R_s = R₁+ R₂ + R₃ + .... + R_n

dengan n banyaknya R yang disusun.

Contoh rangkaian resisitor seri:
1. Hitung nilai resistor pengganti dari ketiga resistor yang dirangkai seperti di bawah ini !

Penyelesaian:

Diketahui: R₁ = 2 ohm
R₂ = 4 ohm
R₃ = 3 ohm
Ditanyakan: Rs = ........ ?
Dijawab :

R_s = R₁+ R₂ + R₃

R_s = 2 + 4 + 3

R_s = 9
Jadi nilai resistor pengganti adalah 9 ohm.

2. Rangkaian Resistor Paralel

Resistor yang disusun secara paralel selalu menghasilkan resistansi yang lebih kecil. Pada rangkaian paralel arus akan terbagi pada masing-masing resistor pada masing-masing resestor, tetapi tegangan pada ujung-ujung resistor sama besar.

Pada rangkaian fresestor disamping untuk R₁, R₂, dan R₃ disusun secara paralel, resistansi dari gabungan R₁, R₂, dan R₃ dapat diganti dengan satu resistor pengganti yaitu Rp.

Resistor yang dirangkai secara paralel mempunyai nilai pengganti, yang besarnya dapat dirumuskan:

1/ R_p = 1/R₁ + 1/R₂ + 1/R₃ + .... + 1/R_n

Jika semua nilai R yang disusun sama besar, maka resistor penggantinya dapat ditulis:

R_p = R / n

dengan n banyaknya R yang disusun.

Contoh menghitung rangkaian resistor paralel:

Hitung nilai resistor pengganti yang dirangkai seperti di bawah ini !

a.

b.

Penyelesaian:
a) Diketahui:

R₁ = 20 ohm
R₂ = 30 ohm
R₃ = 60 ohm

Ditanyakan: Rp = ........ ?

Dijawab:

1/ R_p = 1/R₁ + 1/R₂ + 1/R₃

1/ R_p = 1/20 + 1/30 + 1/30

1/ R_p = 3/60 + 2/60 + 1/60

1/ R_p = 6/60
R_p = 10 ohm

Jadi nilai resistor pengganti adalah 10 ohm.

Penyelesaian:
b) Diketahui:

R₁ = 6 ohm
R₂ = 2 ohm
R₃ = 4 ohm
R6 = 6 ohm

Ditanyakan: R_p = ........ ?
Dijawab:

Seri antara resistor 2 ohm dan 4 ohm

R _s = 2 + 4
R _s = 6

Sehingga rangkaian dapat diganti ini :

Paralel antara 6 ohm, 6 ohm, dan 6 ohm

1/ R_p = 1/R₁ + 1/R₂ + 1/R₃

1/ R_p = 1/6 + 1/6 + 1/6

1/ R_p = 3/6

R_p = 2 ohm

Karena nilai dari masing-masing resistor sama yaitu 6 ohm, maka dapat juga dihitung dengan:

R_p = R / n

R_p = 6 / 3

R_p = 2 ohm

Jadi nilai resistor pengganti adalah 2 ohm